Oprócz histogramów 1-wymiarowych ROOT dysponuje również histogramami 2 i 3 wymiarowymi. Jeśli chodzi o więcej wymiarów to na pomoc przychodzi klasa THnSparse ale osobiście nigdy jej nie używałem więc pominę ją w tym tutorialu. Wynika to z tego, że wraz z liczba wymiarów rośnie szybko rozmiar histogramów, a w większości wypadków i tak większość binów jest pusta.
Histogramy 2D
Reprezentowane przez klasy typu TH2*, i tak np. TH2D reprezentuje 2 wymiarowy histogram z liczbami typu double. Rozważmy sytuację, gdy chcemy wypełnić histogram dwuwymiarowym gausem. Możemy tu użyć funkcji TF2 - reprezentuje ona funkcję dwuwymiarową (o funkcjach będzie więcej przy okazji omówienia fitowania). Przy jej pomocy wypełniamy histogram 2D. Kod przykładu znajduje się poniżej.
Double_t dwugaus(Double_t *x, Double_t *par){
return par[0]*(TMath::Gaus(x[0],par[1],par[2])+TMath::Gaus(x[1],par[1],par[2]));
}
void dwuwymiar(){
gStyle->SetPalette(kRainBow);
TCanvas *c1 = new TCanvas("c1","Graph Example",200,10,700,500);
TH2D *histogram = new TH2D("name","title",100,-1.0,1.0,100,-1.0,1.0);
TF2 *funkcja = new TF2("gausowa",dwugaus,-1.0,1.0,-1.0,1.0,3);
funkcja->SetParameter(0,2.0);
//wartości średnie gausów
funkcja->SetParameter(1,0.0);
//sigma gausów
funkcja->SetParameter(2,0.5);
for(Int_t i=1;i<=GetNbinsX();i++){
for(Int_t j=1;j<=GetNbinsY();j++){
Double_t xval = histogram->GetXaxis()->GetBinCenter(i);
Double_t yval = histogram->GetYaxis()->GetBinCenter(j);
histogram->SetBinContent(i,j,funkcja->Eval(xval,yval));
}
}
histogram->Draw("lego2");
}
W kodzie powyżej tworzymy funkcję dwugaus, ona jest standardową funkcją, która jest przekazywana to TF2. TF2 symbolizuje "matematyczna funkcję dwuwymiarową". W konstruktorze TF2 podajmy jako jeden z argumentów nazwę funkcji "programistycznej" (tj. dwugaus). Funkcja "programistyczna" zwraca wartość w danym punkcie, a jako parametry przyjmuje dwa wskaźniki. Funkcja programistyczna zawsze ma dwa wskaźniki - pierwszy to tablica argumentów funkcji (tutaj x[0] = to nasz x a x[1] to nasz y), drugi argument to tablica parametrów (par[0] to pierwszy parametr, par[1] to drugi itd.).
Następnie ustawiamy parametry naszej funkcji i robimy pętlę po binach, Eval zwraca wartość funkcji. Na końcu zaś rysujemy histogram. gStyle->SetPalette odpowiada za "styl kolorystyczny" rysowanych histogramów.
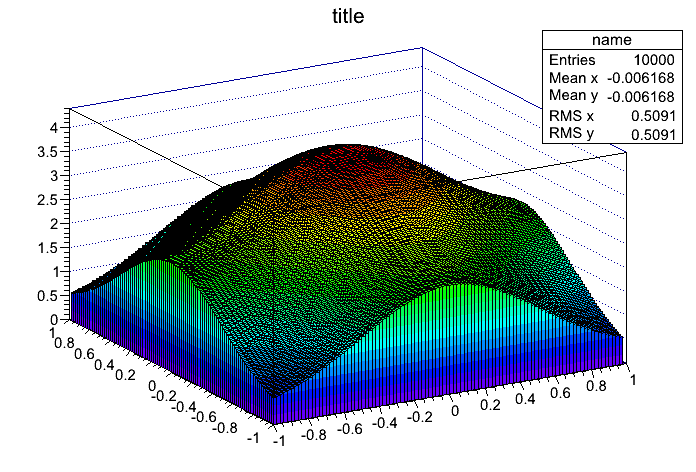
Rys.1 Histogram 2-wymiarowy wypełniony funkcją gaussa.
Histogramy 3D
Są one reprezentowane przez klasy typu TH3*. I tak TH3D reprezentuje histogram ze zmiennymi typu double. Przykład makra tworzącego taki histogram poniżej:
Double_t trojgaus(Double_t *x, Double_t *par){
return par[0]*(TMath::Gaus(x[0],par[1],par[2])+TMath::Gaus(x[1],par[1],par[2])
+TMath::Gaus(x[2],par[1],par[2]));
}
void trojwymiar(){
gStyle->SetCanvasPreferGL(true);
TCanvas *c1 = new TCanvas("c1","Graph Example",200,10,700,500);
TH3D *histogram = new TH3D("name","title",50,-1.0,1.0,50,-1.0,1.0,50,-1.0,1.0);
TF3 *funkcja = new TF3("gausowa",trojgaus,-1.0,1.0,-1.0,1.0,-1.0,1.0,3);
funkcja->SetParameter(0,2.0);
//wartości średnie gausów
funkcja->SetParameter(1,0.0);
//sigma gausów
funkcja->SetParameter(2,0.5);
for(Int_t i=0;iGetNbinsX();i++){
for(Int_t j=0;jGetNbinsY();j++){
for(Int_t k=0;kGetNbinsZ();k++){
Double_t xval = histogram->GetXaxis()->GetBinCenter(i);
Double_t yval = histogram->GetYaxis()->GetBinCenter(j);
Double_t zval = histogram->GetZaxis()->GetBinCenter(k);
histogram->SetBinContent(i,j,k,funkcja->Eval(xval,yval,zval));
}
}
}
histogram->Draw("glcol");
}
Jak widać kod wygląda bardzo podobnie do histogramu 2D z tą różnicą że włączono używanie OpenGL w rysowaniu histogramu (linia 6).
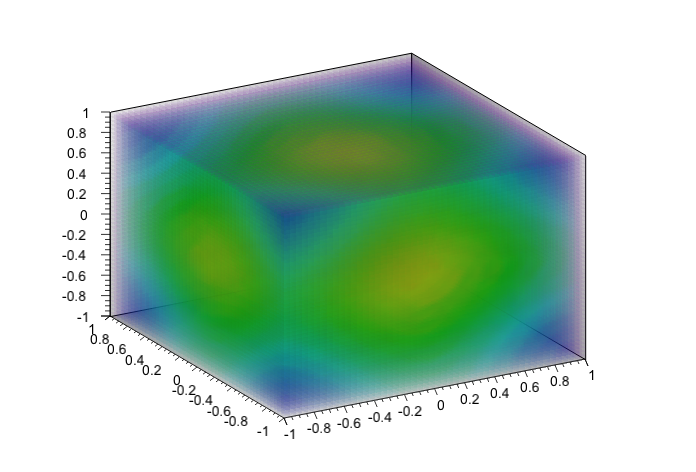
Rys. 2. Histogram 3D z OpenGL.
Można również rysować histogram 3D z użyciem "brył".
// Display a 3D histogram using GL (box option).
//Author: Timur Pocheptsov
void glh3c()
{
gStyle->SetCanvasPreferGL(kTRUE);
TGLTH3Composition * comp = new TGLTH3Composition();
TH3F * h1 = new TH3F("h1", "h1", 10, -1., 1., 10, -1., 1., 10, -1., 1.);
h1->SetFillColor(kRed);
TH3F * h2 = new TH3F("h2", "h2", 10, -1., 1., 10, -1., 1., 10, -1., 1.);
h2->SetFillColor(kGreen);
TH3F * h3 = new TH3F("h3", "h3", 10, -1., 1., 10, -1., 1., 10, -1., 1.);
for(int i=0;i<10000;i++){
h1->Fill(gRandom->Gaus(0,1), gRandom->Gaus(0,1), gRandom->Gaus(0,1));
h2->Fill(gRandom->Gaus(0.5,1), gRandom->Gaus(0.5,1), gRandom->Gaus(0.5,1));
h3->Fill(gRandom->Gaus(-0.5,1), gRandom->Gaus(-0.5,1), gRandom->Gaus(-.5,1));
}
h3->SetFillColor(kBlue);
comp->AddTH3(h1);
comp->AddTH3(h2, TGLTH3Composition::kSphere);
comp->AddTH3(h3);
comp->Draw();
TPaveLabel *title = new TPaveLabel(0.04, 0.86, 0.96, 0.98,
"TH3 composition.");
title->SetFillColor(32);
title->Draw();
}
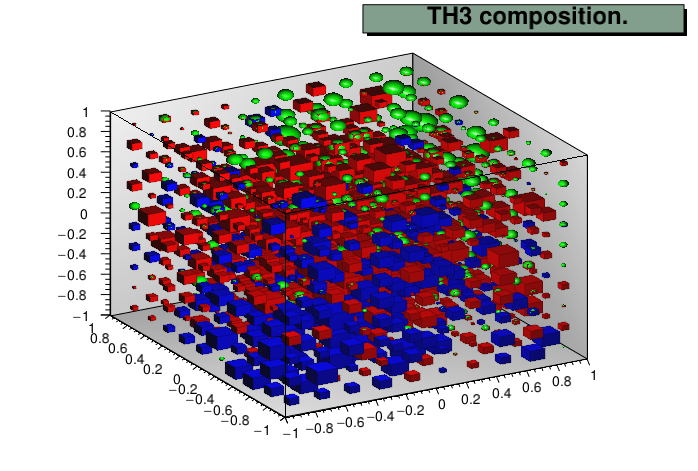
Rys. 3 Histogram 3D "z bryłami".
Projekcje
Ważną operacją przy operowaniu na histogramach są tzw. projekcje czyli umiejętność "wycięcia" części histogramu. Przykładowo poniżej pokazano jak rysować "plasterki 1-wymiarowe z dwuwymiarowego histogramu".
Double_t dwugaus(Double_t *x, Double_t *par){
return par[0]*(TMath::Gaus(x[0],par[1],par[2])+TMath::Gaus(x[1],par[1],par[2]));
}
void Tomograf(){
TCanvas *c1 = new TCanvas("c1","Graph Example",200,10,700,500);
c1->Divide(2,1);
TH2D *histogram = new TH2D("name","title",100,-1.0,1.0,100,-1.0,1.0);
TH1D *slice = new TH1D("skan","skan",100,-1,1);
TF2 *funkcja = new TF2("gausowa",dwugaus,-1.0,1.0,-1.0,1.0,3);
funkcja->SetParameter(0,2.0);
//wartości średnie gausów
funkcja->SetParameter(1,0.0);
//sigma gausów
funkcja->SetParameter(2,0.5);
for(Int_t i=0;iGetNbinsX();i++){
for(Int_t j=0;jGetNbinsY();j++){
Double_t xval = histogram->GetXaxis()->GetBinCenter(i);
Double_t yval = histogram->GetYaxis()->GetBinCenter(j);
histogram->SetBinContent(i,j,funkcja->Eval(xval,yval));
}
}
c1->cd(1);
histogram->Draw("lego2");
c1->cd(2);
for(Int_t i=0;iGetNbinsY();i++){
slice=histogram->ProjectionX("projekcja",i,i+1);
slice->Draw();
c1->Update();
//czekaj 100 ms między projekcjami
gSystem->Sleep(100);
}
}
Najważniejszą częścią jest metoda TH2D::ProjectionX która pobiera projekcję. Należy tutaj zwrócić uwagę na dwie ważne rzeczy:
- projekcja jest pobierana na podstawie numeru binu a nie wartości na osi X
- projekcja powinna mieć unikalną nazwę jeśli chcemy rysować kilka projekcji, inaczej ostatnia o danej nazwie nadpisuje wszystkie poprzednie o tej samej nazwie
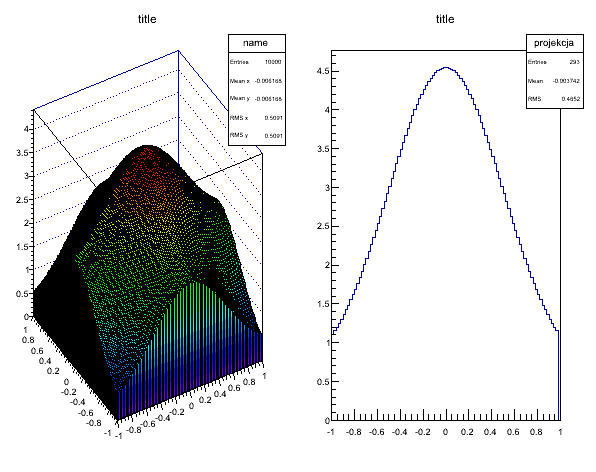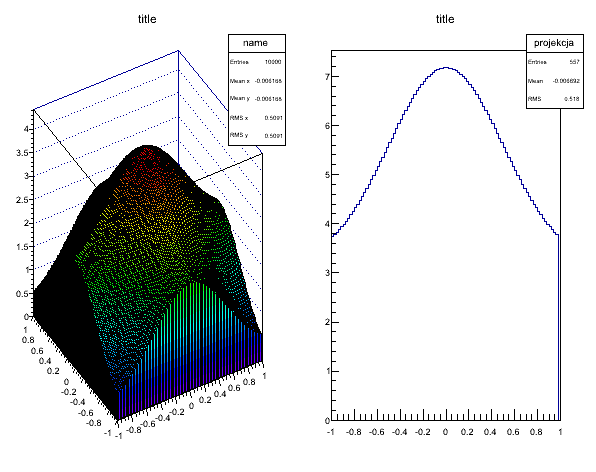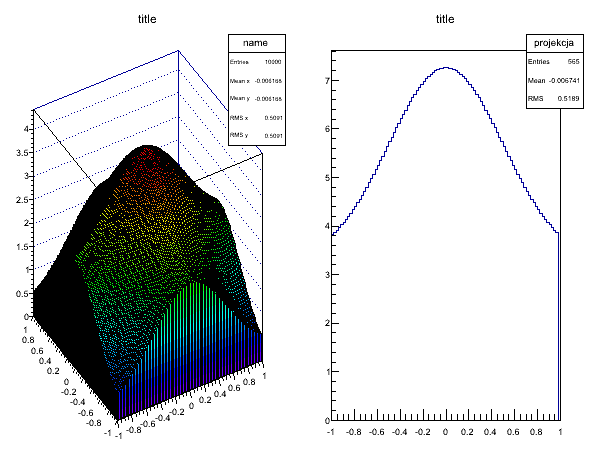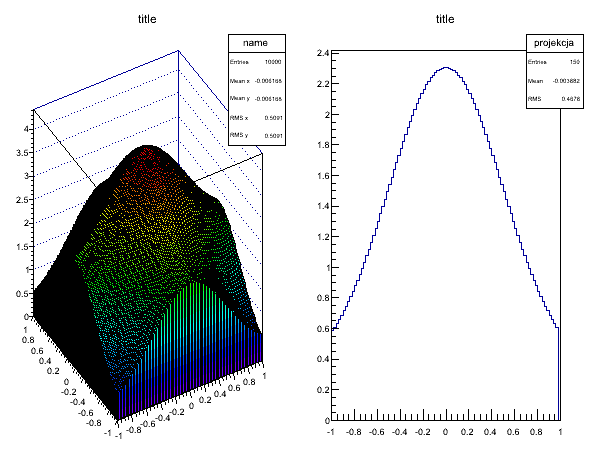
Rys. 4. Histogram 3D z animacją projekcji.
Jednoczesne rysowanie histogramów
Kolejnym problemem jest rysowanie kilku histogramów obok siebie. Poniżej rysunek i makro próbujące narysować dwa TH2D razem:
void fill(TH2D *h1,TH2D *h2){
for(Int_t i=1;iGetNbinsX();i++){
for(Int_t j=1;jGetNbinsX();j++){
if((i<=20&&j<20)||(i>20&&j>20)){
h1->SetBinContent(i,j,1);
}else{
h2->SetBinContent(i,j,1);
}
}
}
}
void two_dim(){
TCanvas *c1 = new TCanvas();
c1->Divide(1,2);
TH2D *h1 = new TH2D("h1","h1",40,0,1,40,0,1);
h1->SetFillColor(kRed);
TH2D *h2 = new TH2D("h2","h2",40,0,1,40,0,1);
h2->SetFillColor(kWhite);
fill(h1,h2);
c1->cd(1);
h1->Draw("lego1");
h2->Draw("SAME+lego1");
c1->cd(2);
THStack *stack = new THStack();
stack->Add(h1);
stack->Add(h2);
stack->Draw();
}
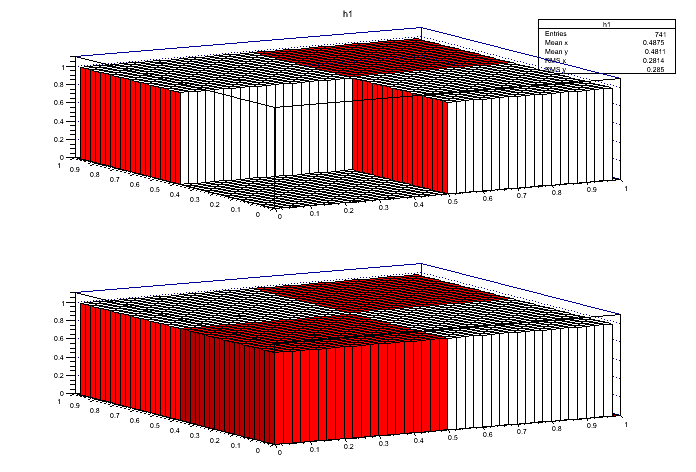
Rys. 5. Histogramy 2D rysowane razem
W makrze podjęto próbę rysowania dwóch histogramów (białego i czerwonego), po zsumowaniu powinny dać biało-czerwoną szachownicę. Gdy użyto metody "SAME" (górny pad) wyraźnie widać że "dolna ćwiartka" nie jest wypełniona, nie jest wypełniona również górna ćwiartka - tak naprawdę czerwony obszar rysowany na górze pochodzi od "ścianek" histogramu, a nie od wypełnienia. Oznacza to, że w przypadku rysowania metodą "SAME" dla dwóch wymiarów drugi (i kolejne) histogramy nie są tak naprawdę rysowane.
Na dolnym padzie użyto metody z użyciem THSTack, dzięki temu narysowana jest suma histogramów.
Należy tu zwrócić uwagę że THStack nie jest idealnym odpowiednikiem metody "SAME", THStack został zaprojektowany głównie do rysowania "zsumowanych histogramów", a nie histogramów nałożonych na siebie tak jak to robi "SAME". Najłatwiej to wyjaśnić na poniższym makrze i rysunku gdzie wyraźnie widać że THSTack to suma histogramów a nie to samo co SAME.
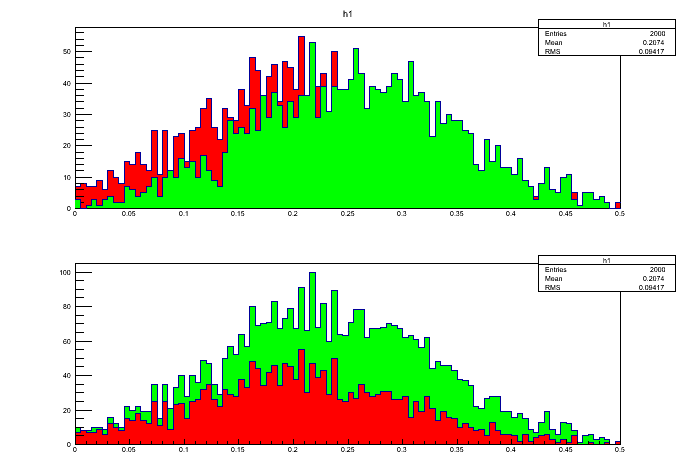
Rys. 6 Histogramy TH1D narysowane metodą "SAME" (u góry) oraz z użyciem THStack. Poniżej makro pozwalające uzyskać te obrazki.
void generator(TH1D *h, Double_t mean, Double_t sigma, Int_t times){
for(Int_t i =0;i<times;i++){
h->Fill(gRandom->Gaus(mean,sigma));
}
}
void one_dim(){
TCanvas *c1 = new TCanvas();
c1->Divide(1,2);
c1->cd(1);
TH1D *h1 = new TH1D("h1","h1",100,0,0.5);
h1->SetFillColor(kRed);
TH1D *h2 = new TH1D("h2","h2",100,0,0.5);
h2->SetFillColor(kGreen);
generator(h1,0.2,0.1,2000);
generator(h2,0.25,0.1,2000);
h1->Draw();
h2->Draw("SAME");
c1->cd(2);
THStack *stack = new THStack();
stack->Add(h1);
stack->Add(h2);
stack->Draw();
}