Jedną z ważniejszych umiejętności jaka się przydaje w analizie danych jest fitowanie czyli dopasowywanie danych.
Czym w zasadzie jest fitowanie danych? Zasadniczo polega ono na tym, że mamy dane, jakąś funkcję z parametrami i szukamy minimalnej wartości funkcji "niepodobieństwa" między funkcją dopasowywaną a danymi. Gdy znajdziemy minimum tej funcji oznacza to, że każdy inny zestaw parametrów jest gorszy. Zwykle tą funkcją "niepodobieństwa" jest tzw. chi-kwadrat.
Prosty fit
Do najprostszego fitu można użyć klasy TF1, poniżej zamieszczono minimalny przykład:
//tworzy histogram
TH1D *GetRandomHist(){
TH1D *h = new TH1D("h","h",100,-2,2);
for(int i=0;i<1000;i++){
h->Fill(gRandom->Gaus(0, 0.5));
}
return h;
}
//nasza dopasowywana funkcja
Double_t Func(Double_t *x, Double_t *p){
return p[0]*TMath::Exp(-x[0]*x[0]/(2.0*p[1]*p[1]));
}
void fit2(){
TH1D *h = GetRandomHist();
Double_t funcRangeMin = -1;
Double_t funcRangeMax = 1;
Int_t nParams = 2;
TF1 *f = new TF1("func",Func,-funcRangeMin,funcRangeMax,nParams);
/*niestety ROOT ma problem z fitowaniem i trzeba mu pomóc ze
znalezieniem parametrów fitu*/
f->SetParLimits(0,10,100);
f->SetParLimits(1,0.2,1);
f->SetRange(-0.4, 0.4);
h->Fit(f);
}
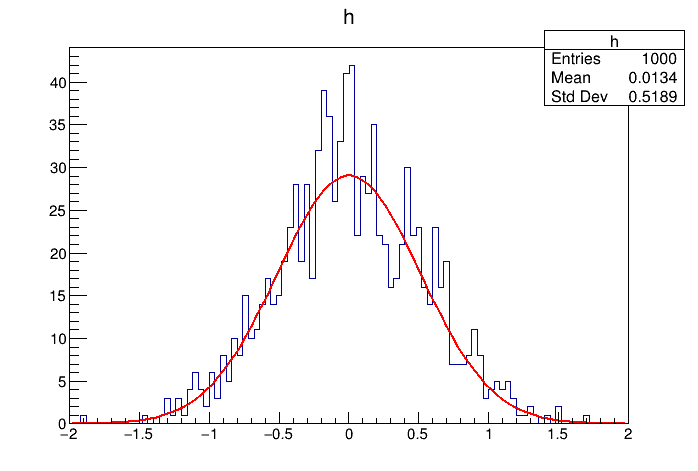
W przykładzie tym tworzymy klasę TF1, drugim argumentem jest wskaźnik na funkcję Func. Funkcja taka musi mieć dokładnie taką strukturę jak zaprezentowano w przykładzie tzn. zwraca double, przyjmuje za parametr dwa wskaźniki na double. Zwracana wartość to po prostu wartość dopasowywanej funkcji. Pierwszy wskaźnik to tablica argumentów funkcji np. dla funkcji dwuwymiarowej x[0] odpowiadałoby X-owi a x[1] -Y-owi. Drugi wskaźnik to tablica kolejnych parametrów i tak p[0] - to pierwszy parametr a p[1] - to drugi parametr (sigma rozkładu gaussa). Następnie w konstruktorze TF1 podajemy dziedzinę funkcji i liczbę parametrów.
Często jednak zdarza się że funkcja fitująca nie potrafi znaleźć dopasowania, konieczne wtedy staje się udzielenie ROOTowi "pomocy". Pomoc ta polega np. na zawężeniu wartości dozwolonych parametrów. Lista najważniejszych funkcji w klasie TF1 zaprezentowana jest poniżej.
| Funkcja | Opis |
| FixParameter(Int_t par_no, Double_t val) | ustawia parametr |
| SetParLimits(Int_t par, Double_t min, Double_t max) | ustawia zakres parametru |
| SetParameter(Int_t par, Double_t vale) | ustawia dany parametr (ale tylko wartość startową, po fitowaniu wartość ta może być inna) |
| SetParName(Int_t par, const char *name) | ustawia nazwę parametru |
| GetNDef() | zwraca liczbę stopni swobody |
| GetParameter(Int_t par) | zwraca wartość parametru |
| GetParError(Int_t par) | zwraca błąd parametru |
| GetChiSquare() | zwraca wartość chi2 |
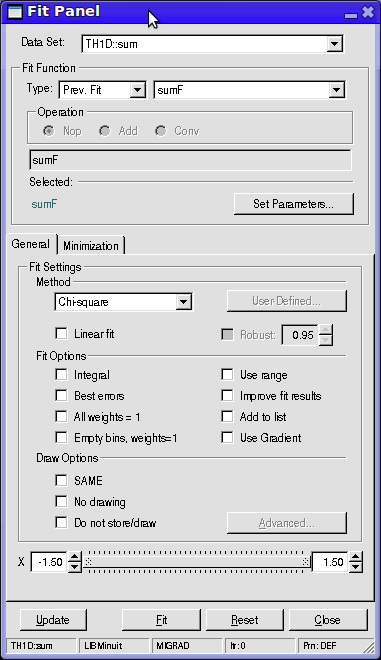
W bardziej złośliwym przypadku nie mamy pojęcia o tym jakie wartości może mieć dany parametr, w takim przypadku można użyć ROOTowego GUI. Polega to na tym że uruchamiamy makro fitujące ale potem w pasku nad histogramem z Tools wybieramy Fit Panel. Przy pomocy Fit panelu możemy "ręcznie dopasować histogram", tak aby na oko oszacować zakresy wartości parametrów. Taki panel może wyglądać jak poniżej. Gdy fitujemy kilka histogramów/kilka funkcji warto tu zwrócić uwagę na pole Data Set i Fit Function - aby upewnić się fitujemy właściwe dane właściwymi funkcjami.
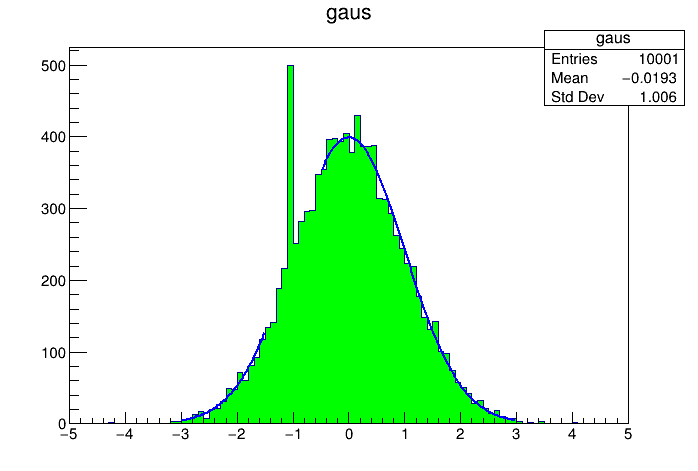
Analogicznie do fitowania histogramów 2 i 3D są odpowiednio TF2 i TF3. Innym problemem jaki może się wydarzyć jest konieczność ominięcia jakiegoś obszaru fitowania , w tym wypadku do wykluczenia pewnego obszaru wystarczy TF1::RejectPoint():
TH1D* histo1(){
TH1D *histo = new TH1D ("gaus","gaus",100,-5,5);
histo->FillRandom("gaus",10000);
histo->SetBinContent(40,500);
histo->SetFillColor(kGreen);
return histo;
}
//funkcja
Double_t fitter (Double_t *x, Double_t *params){
Double_t mean = params[1];
Double_t norm = params[0];
Double_t sigma = params[2];
//ignorowanie pewnego obszaru
if(x[0]<-0.5&&x[0]>-1.5){
TF1::RejectPoint();
return 0;
}
return norm*TMath::Exp(-((x[0]-mean)*(x[0]-mean))/2.0/sigma/sigma);
}
void fit(){
TH1D *h = histo1();
TF1 *f = new TF1("fun",fitter,-3.0,3.0,3);
//te funkcje są "ucięte" dzięki czemu nie będzie problemu z ich rysowaniem
TF1 *f_draw = new TF1("fun2",fitter,-0.5,3,3);
TF1 *f_draw2 = new TF1("fun22",fitter,-3,-1.5,3);
f->FixParameter(1,0);
f->SetParameter(0,100);
f->SetParLimits(2,0.0001,10000);
f->SetParName(0,"norm");
f->SetParName(1,"mean");
f->SetParName(2,"sigma");
f->SetLineColor(kRed);
//dzięki N - nie wyświetla się stara funkcja
h->Fit(f,"RQN");
//przepisywanie parametrów funkcji wejściowej na funkcje "ucięte"
for(int i=0;i<3;i++){
f_draw->SetParameter(i,f->GetParameter(i));
f_draw2->SetParameter(i,f->GetParameter(i));
}
f_draw->SetLineColor(kBlue);
f_draw2->SetLineColor(kBlue);
h->Draw();
//rysuj urwana funkcję jako "dwa kawalki"
f_draw->Draw("SAME");
f_draw2->Draw("SAME");
}
TVirtualFitter
TVirtualFitter to klasa używana do fitowania obok klasy typu TF1. Klasa ta jest bardziej skomplikowana w użyciu, ale jednocześnie dużo potężniejsza. W przypadku TF1 mogliśmy w zasadzie minimalizować jedynie chi2 lub inną predefiniowaną funkcję, TVF umożliwia minimalizowanie praktycznie dowolnej funkcji, jest to bardzo przydatne w przypadkach typu:
- fitowanie które nie jest minimalizacją predefiniowanych "funkcji nieprawdopodobieństwa" typu chi2
- fitowanie bardziej zaawansowanych danych - np. dwóch histogramów jednocześnie
- wyznaczenie wartości minimalizowanej funkcji jest szybsze/łatwiejsze niż podanie formuły na jej wartość w dowolnym punkcie
W przypadku TVF nie podajemy funkcji którą chcemy dopasować a funkcję którą chcemy MINIMALIZOWAĆ, jeśli więc chcemy dopasować "zwykłym chi2" dwa histogramy nasza minimalizowana funkcja powinna zwracać wartość chi2 a nie dopasowywanej funkcji. Poniżej przykład użycia fittera. Należy zwrócić uwagę że nie tworzymy nowego fittera, a raczej odwołujemy się istniejącego obiektu, następnie podajemy jako argument (SetFCN) funkcję którą chcemy minimalizować. Podobnie jak w TF1 funkcja ta ma określoną strukturę: pierwszy argument to liczba parametrów, drugi to dane, trzeci to wartość f którą chcemy zminimalizować, par to parametry - niestety nie wiem czym jest ostatni int. W kodzie poniżej staramy się znaleźć x dla którego funkcja paraboliczna przyjmuje minimum.
Double_t a,b,c;
void myfcn(Int_t &, Double_t *, Double_t &f, Double_t *par, Int_t) {
f =0;
Double_t x =par[0];
f= a*x*x+b*x+c;
}
void fit2(){
TVirtualFitter::SetDefaultFitter("Minuit");
TVirtualFitter *vF = TVirtualFitter::Fitter(0,1);
vF->SetFCN(myfcn);
a=1.9;
b=-0.6;
c=0.5;
Double_t arglist[1] = {0};
vF->SetParameter(0,"a",0,10.5,-1,1);
vF->ExecuteCommand("MIGRAD", arglist, 0);
Double_t par = vF->GetParameter(0);
cout<<"Fitter result"<<endl;
cout<<"Found :"<<endl;
cout<<Form("%4.4f",par)<<endl;
cout<<"Expected"<<endl;
cout<<Form("%4.4f",-b/2.0/a)<<endl;
}
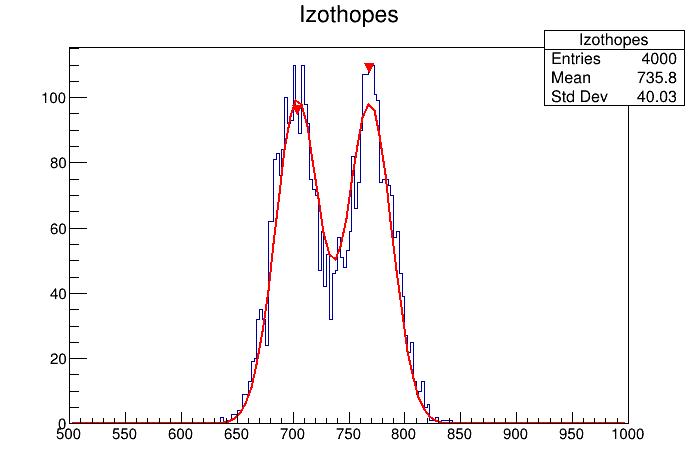
TSpectrum
TSpectrum jest czymś czego w zasadzie nigdy nie używałem ale warto być świadomym że coś takiego istnieje. W przeciwieństwie do wyżej wymienionych klas które służą dopasowywaniu funkcji głównym zadaniem tej funkcji jest m. in. znajdowanie pików. Poniżej przykład zastosowania tej klasy w celu dofitowania dwóch gaussów, znalezione piki oznaczono trójkątami.
Double_t func(Double_t *x, Double_t *params){
Double_t f1 = TMath::Gaus(x[0],params[0],params[1])*params[2];
Double_t f2 = TMath::Gaus(x[0],params[3],params[4])*params[5];
return f1+f2;
}
void piki(){
TH1D *tg = new TH1D ("Izothopes","Izothopes",200,500,1000);
TF1 *f = new TF1("f",func,0,1000,6);
f->SetParLimits(0,600,800);
f->SetParLimits(1,10,800);
f->SetParLimits(2,50,800);
f->SetParLimits(3,600,800);
f->SetParLimits(4,10,800);
f->SetParLimits(5,50,800);
for(Int_t i=0;i<2000;i++)
tg->Fill(gRandom->Gaus(770,20));
for(Int_t i=0;i<2000;i++)
tg->Fill(gRandom->Gaus(700,20));
//szukaj maksymalnie 4 piki
TSpectrum *spec = new TSpectrum(4);
//szukany histogram, oczekiwana signma, opcje poszukiwań, próg poszukiwań
Int_t nfound = spec->Search(tg,2,"",110.10);
Double_t *peak =spec->GetPositionX();
f->FixParameter(0,peak[0]);
f->FixParameter(3,peak[1]);
TCanvas *c1 = new TCanvas();
tg->Fit(f);
tg->Draw();
}