Drzewa ROOTowe
Na poprzedniej lekcji pokazałem jak zapisywać proste obiekty do drzew ROOTowych. Ale tak naprawdę nie opcja zapisywania danych do drzewa jest największym ficzerem ROOTa, największym ficzerem są tzw. drzewa ROOTowe.
Drzewo ROOTowe można uznać za coś w rodzaju tabeli z wejściami. Wejście odpowiada np. jednemu zarejestrowanemu zderzeniu. Pojedyncze wejście może zawierać wiele tzw. gałęzi tzn. wiele różnych klas. Głównymi zaletami drzew są:
- automatyczne zarządzanie pamięcią, użytkownik tylko na początku podłącza się pod określoną gałąź, następnie po wywołaniu TTree::GetEntry wskaźnik pod który podłączyliśmy się jest nadpisywany nowym wejściem
- wczytywanie obiektów, zasadniczo o ile stworzymy słownik dla danej klasy nie musimy się troszczyć o sam odczyt i zapis danych
- zużycie pamięci - drzewo nigdy nie jest wczytywane w całości dzięki czemu nawet wielkie drzewo może być analizowane z użyciem niewielkich zasobów
- wyłączanie branchy, czytanie wejść - w ROOT można wyłączyć wczytywanie okreśłonych branchy w zderzeniu - dzięki temu nie musimy wczytywać niepotrzebnych danych, co więcej wczytanie n-tego zderzenia nie wcale nie oznacza konieczności czytania n-1 poprzedzających go zderzeń
NTuple
Drzewa powstały aby przechowywać złożone struktury - np. kilka różnych klas, NTuple to uproszczona wersja drzew - zawiera ona po prostu klika liczby zmiennoprzecinkowych w wejściu. Tworzenie tego typu obiektów jest bardzo proste, przykładowo chcąc zapisać 3 wartości liczbowe tworzymy można użyć makra:
void ntuple(){
TFile *file = new TFile("data.root","recreate");
TNtuple *ntup = new TNtuple("data","title","x:y:z");
for(int i=0;i<100;i++){
Float_t x = gRandom->Gaus(0,1);
Float_t y = gRandom->Gaus(0,1);
Float_t z = gRandom->Gaus(0,1);
ntup->Fill(x,y,z);
}
file->Write();
file->Close();
};
Najpierw w makrze tym otwieramy plik, potem tworzymy TNtuple, gdzie podajemy nazwę i tytuł TNtupla, następnie podajemy oddzielone dwukropkiem nazwy "liści", tutaj mamy trzy zmienne x,y,z dlatego w przypadku TNtuple w konstruktorze wpisujemy "x:y:z". Następnie w pętli wypełniamy ntuple danymi, następnie zapisyujemy je i zamykamy plik.
Odczyt takiego drzewka jest relatywnie prosty:
void ntupleR(){
TFile *file = new TFile("data.root");
TNtuple *ntup = (TNtuple*)file->Get("data");
Float_t *arr = ntup->GetArgs();
for(int i=0;iGetEntries();i++){
ntup->GetEntry(i);
cout<<arr[0]<<" "<<arr[1]<<" "<<arr[2]<<endl;
}
}
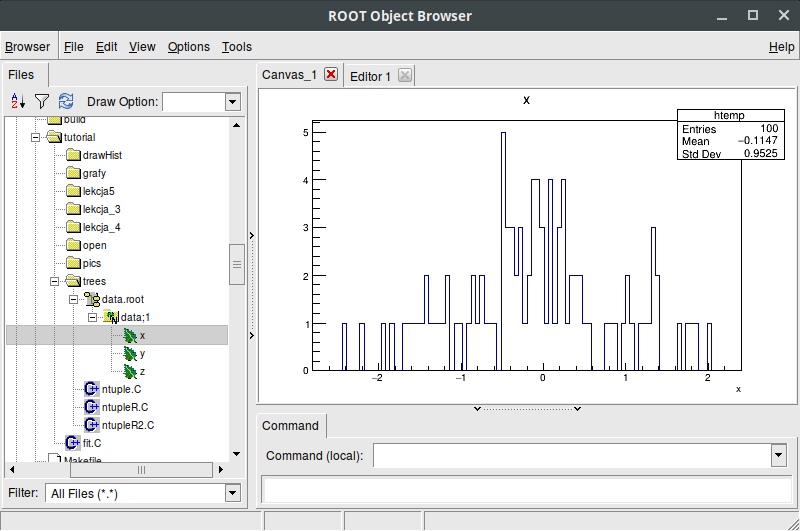
Rys. 1. Przykładowy widok z TBrowsera na TNtuple. Widać trzy "liście" reprezentujące trójkę liczb zapisywanych w każdym wejściu.
W tym przypadku arr to tablica zawierająca kolejne argumenty ntupla (np. arr[0] to nasze x a arr[1] to y). Istnieje jeszcze inna metoda odczytu danych - od razu z wizualizacją:
void ntupleR2(){
TFile *file = new TFile("data.root");
TNtuple *ntup = (TNtuple*)file->Get("data");
ntup->Draw("x+y","x>0 && y>0");
}
W tym przypadku użyjemy TNtuple::Draw, pierwszy argument mówi co chcemy narysować, podczas gdy drugi nakłada dodatkowy warunek na to, jaki zbiór danych chcemy narysować.
TTreeViewer
TTreeViewer to trochę bardziej wypasiona wersja TBrowsera, umożliwia ona trochę bardziej zaawansowane przeglądanie pliku. Aby stworzyć TTreeViewer uruchamiamy najpierw TBrowser, następnie klikamy na interesujące nas drzewo i klikamy z rozwijanego menu na StartViewer, wtedy pojawi się coś takiego:
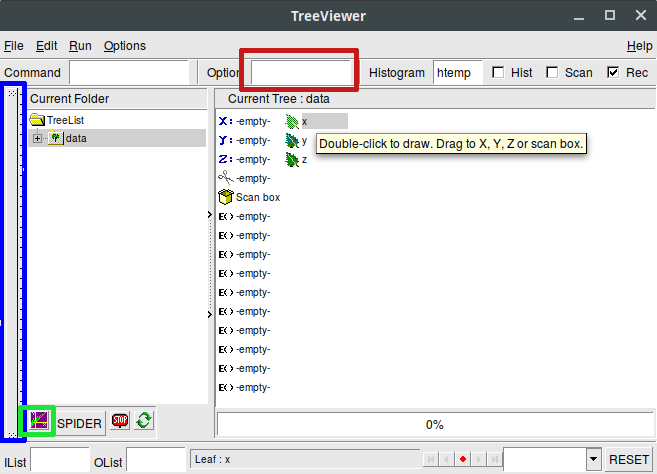
Rys.2 TTreeViewer
Na rysunku powyżej widać TTReeViewer (TTRV), co tu widzimy? Niebieską ramką zaznaczono suwak który odpowiada za to jaki zakres drzewa przeglądamy (tutaj domyślne całe drzewo). Kolorem zielonym oznaczono guzki którym zatwierdzamy rysowanie histogramów (pojawią się w TBrowser którym stworzyliśmy TTreeViewer). Czerwone pole to opcja rysowania (działa tak jak przy rysowaniu zwykłych histogramów). Z lewej strony widzimy też strukturę drzewa. Struktura ta być trochę inna niż ta w TBrowser np. TLorentzVector posiada widoczne pola fP i fE w TTreeViewer podczas gdy TBrowser pokazuje pola typu Px, Py, itd.). Tak różnica wynika prawdopodobnie z tego, że TBrowser patrzy bezpośrednio na TLorentzVector podczas gdy TTreeViewer widzi go jako klasę dziedziczącą po TVector3.
Teraz czas na pytanie co nam to daje? Ano to, że możemy sobie rysować pewne wielkości bez pisania makr. I tak w okienku po lewej widzimy trzy "listki" symbolizujące pola x,y,z, obok widzimy niebieskie litery X,Y,Z (nazwijmy to pole rysowania), poniżej nożyczki, potem scan box box i E() czyli wyrażenia. I tutaj podam przykłady pewnych prostych operacji rysowania.
Rysowanie części danych
W TBrowserze, gdy kliknęliśmy w branch x rysowaliśmy całą zawartość brancha x. W TTRV możemy przeglądać jedynie fragment drzewa. Jak to działa? Najpierw przeciągamy listek x na pole rysowania X, następnie klikamy na guzik rysowania - widzimy to co w TBrowserze, ale jeśli zaczniemy manipulować suwakiem (oznaczonym na rys.2 na niebiesko) zauważymy, że za każdym rysowaniem liczba wejść w histogramie zmienia się - np. jeśli suwak będzie od góry do połowy - przeczytamy pierwszą połowę pliku.
Rysowanie wielowymiarowe
Ok a teraz co jeśli chcemy wyrysować histogram 2d np. x vs y? Wtedy wystarczy przeciągnąć listek x na pole rysowania X a listek y na pole rysowania Y, klikamy guzik rysowania i zrobione. Niestety dostaniemy czarne kropki, dlatego lepiej wpisać w panelu rysowania (czerwona ramka) opcję "colz" lub "lego". Ale to nie koniec, mamy jeszcze wyrażenia. Załóżmy że chcemy narysować sumę x+y vs różnicę x-y. W tym przypadku klikamy dwa razy w jakies pole E(), pojawia się "Expression editor", w górnym polu wpisujemy "x+y" - to nasza formuła na sumę, w dolnym wpiszmy "SUM" (to nasza nazwa sumy), następnie robimy to samo z następnym slotem E(), ale że teraz chcemy różnicę wpisujemy odpowiednio "x-y" oraz "DIF". Następnie przeciągamy jedno wyrażenie na pole rysowania X a drugie na pole rysowania Y, zatwierdzamy i zrobione.
Cięcia
Możemy jeszcze bardziej rozbudować naszą analizę i wzbogacić ją o cięcia. W tym celu klikamy na pole oznaczone nożyczkami i tworzymy nowe wyrażenie np. x>y, klikamy zatwierdź i okaże się że pojawią się tylko takie pary SUM+DIF które spełniają warunek "x>y". Cięcie można włączać i wyłączać (wyłączone cięcie będzie przekreślonymi nożyczkami). Należy tu zauważyć że expression nie tylko operuje na nazwach branchy - ale również na nazwach wyrażeń.
Niewidoczne branche.
Ostatnia uwaga dotyczy rysowania bardziej złożonych obiektów - w następnej lekcji wygenerujemy gałąź z obiektami klasy TLorentzVector. Nie jest to już prosty NTuple, w tym wypadku TTRV nie widzi wszystkich pól które są widoczne w TBrowserze - co więc gdy np. chcielibyśmy narysować rozkład kąta phi? Wystarczy go wyklikać w TBrowserze, wtedy pojawi nam się coś takiego jak na rysunku poniżej, aby uzyskać taki sam rysunek w TTRV musimy użyć wyrażenia które jest tytułem tego histogramu tj. "tracks_global.tracks_global.fP.Phi().
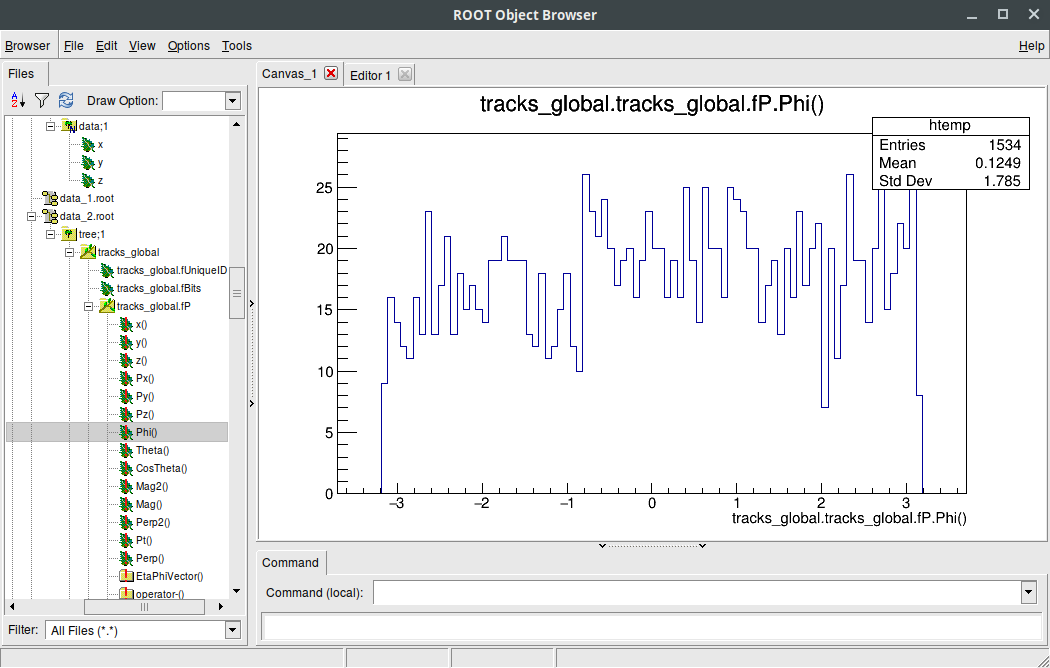
Rys. 3. TTreeViewer nie pokaże nam pola Phi, x, czy y, ale TBrowser je pokazuje, dlatego można użyć TBrowsera do odszukania jakich nazw musimy użyć aby wyświetlić te "ukryte dane".