Dostęp do danych eksperymentalnych wymaga posiadania kont na komputerach używanych przez daną kolaborację. Dla "śmiertelnika" czy nawet studenta uzyskanie tam dostępu jest w najlepszym wypadku czasochłonne.
Podstawowych rzeczy można się nauczyć jednak bez użycia wielkich zasobów, wielkich eksperymentów. Na rynku dostępne są generator MC - programy symulujące proces zderzeń ciężkich jonów. Niektóre są szybkie inne wolne, niektóre złożone inne proste. My do naszych celów będziemy pisać własne proste i szybkie generatory.
Pierwszy generator
Nasz generator zapisywał będzie dane w formacie OTF. Dlatego dobrze będzie zainstalować HAL-a z przykładami (-DEXAMPLES=ON przy kompilacji).
Nasz pierwszy generator będzie generował cząstki z podanym z góry rozkładem zmiennych rapidity i pT. Oto kod:
void simple_mc() {
auto run = new Hal::AnalysisManager();
// tworzenie źródła
auto source = new HalOTF::Source(10);
// tworzenie generatora i danych do generatora
TH2D h("spec", "spec", 1, -1, 1, 1, 0, 1);
h.SetBinContent(1, 1, 1);
auto generator = new HalOTF::EventGenerator();
generator->SetSpiecies(h, Hal::Const::PionPlusPID());
generator->SetFixMult(100);
source->AddEventGenerator(generator);
//zapisuj dane do wyjściowego drzewa
source->Register();
//plik wyjściowy
run->SetOutput("data.root");
run->SetSource(source);
//inicjalizacja analizy
run->Init();
//analiza
run->Run();
}
Na początku tworzymy nasz analizator (AnalysisManager) to klasa zarządzająca symulacjami i analizami w HAL-u. Następnie tworzymy źródło danych - w tym wypadku jest to HalOTF::Source. HalOTF::Source prezentuje źródło danych generowanych w locie (On The Fly - stąd OTF). Samo Hal::OTFSource jednak wygeneruje nam puste zderzenie. Argumentem konstruktora tej klasy jest (maksymalna) liczba zderzeń jakie będa analizowane.
W kolejnym kroku tworzymy histogram z rozkładem pt-y, wypełniamy 1 jego bin (dostaniemy więc płaski rozkład rapidity od -1 do 1 i pędu poprzecznego od 0 do 1 GeV/c). Histogram ten dodajemy do generatora. W SetSpieces określamy histogram y-pt, z którego będą generowane zmienne kinematyczne określające właściwości wyprodukowanych cząstek, określamy też typ cząstek (tu piony dodatnie). FixMult to ustawiona na stałe krotność pionów - tj. liczba tych cząstek na zderzenie. Na końcu dodajemy generator. W ogólności można użyć kilku generatorów.
W linii 13 informujemy że chcemy zapisać dane (domyślnie HalOTF generuje cząstki/zderzenia ale ich nie zapisuje). Następnie określamy nazwę pliku wyjściowego, podłączamy źródło danych do analizy.
Init inicjuje analizę - musi być ZAWSZE wywołane przed Run, który przeprowadza analizę.
Nasz pierwszy generator
W praktyce jednak zdarza się, że chcemy sobie zbudować bardziej spersonalizowany generator. Tutaj użyjemy nieco zmodyfikowanego przykładu - napiszemy własny generator, ale wykorzystując bazową klasę:
class CustomGenerator : public HalOTF::EventGenerator {
protected:
virtual void GenerateEvent() {
Int_t shift = fMcEvent->GetNTracks();
fCurrrentMult = fFixedMultiplicity;
if (fMultiplicity) fCurrrentMult = fMultiplicity->GetRandom();
for (int i = 0; i < fCurrrentMult; i++) {
Double_t pt, y;
fSpectras->GetRandom2(y, pt);
Double_t mt = TMath::Sqrt(pt * pt + fMass * fMass);
Double_t phi = gRandom->Uniform(0, TMath::Pi());
Double_t px = pt * TMath::Cos(phi);
Double_t py = pt * TMath::Sin(phi);
Double_t pz = mt * TMath::SinH(y);
OTF::McTrack tr;
TLorentzVector p;
p.SetXYZM(px, py, pz, fMass);
tr.SetMomentum(p);
tr.SetPdgCode(fPids);
TLorentzVector xr(gRandom->Gaus(0, 1), gRandom->Gaus(0, 1), gRandom->Gaus(0), 0);
tr.SetFreezout(xr);
fMcEvent->AddTrack(tr);
OTF::RecoTrack rtr;
px = px + gRandom->Gaus(0, fSmear) * px;
py = py + gRandom->Gaus(0, fSmear) * py;
pz = pz + gRandom->Gaus(0, fSmear) * pz;
Double_t e = TMath::Sqrt(px * px + py * py + pz * pz + fMass * fMass);
rtr.SetMom(px, py, pz, e);
rtr.SetNHits(5);
rtr.SetCharge(fCharge);
rtr.SetMcIndex(i + shift);
fRecoEvent->AddTrack(rtr);
}
}
public:
CustomGenerator() {};
virtual ~CustomGenerator() {};
};
W naszej klasie w zasadzie podmieniamy tylko metodę GenerateEvent, która to tworzy dane do eventu. Teraz kilka wyjaśnień co się w niej dzieje:
- Najpierw wyliczone jest przesunięcie - to jest indeks ostatniej dodanej cząstki w generatorze (w teorii mogliśmy mieć wywołany wcześniej inny generator).
- Następnie liczymy krotność naszych cząstek, na początku zakładamy, że krotonośc jest stała i równa fFixedMultiplicity. Następnie sprawdzamy czy histogram fMultiplicity (określa rozkład krotności) istnieje, jeśli tak bierzemy losową wartość krotności z niego (fMultiplicity->GetRandom). Oznacza to że histogram ma pierwszeństwo w definiowaniu krotności przed ustawioną na szytwno jedną liczbą.
- Następnie w pętli generowane są cząstki. Tutaj jest cała kinematyka generacji. Warto zauważyć że:
- generujemy tu tak naprawdę cząstki "symulowane" (OTF::McTrack) oraz "zrekonstruowane" (OTF::RecoTrack) które są tak naprawdę cząstkami z rozmytym pędem (linie 26-29).
- używamy zmiennej shift - była ona nam potrzebna do wyliczenia indeksu cząstki MC która będzie złączona z cząstką zrekonstruowaną (SetMcIndex). Przykładowo jeśli wcześniej wygenerowaliśmy 100 cząstek to powinniśmy pierwszą cząstkę "zrekonstruowaną" złączyć ze 101 cząstka symulowaną a nie cząstką 0.
- tym razem phi - kąt azymutalny jest generowany od zera do $\pi$ (w klasie bazowej jest od minus do plus $\pi$
Reszta kodu jest poniżej, rózni się on w zasadzie jedynie użyciem innego generatora - naszej klasy.
void advanced_mc() {
auto run = new Hal::AnalysisManager();
auto source = new HalOTF::Source(10);
auto generator = new CustomGenerator;
TH2D h("spec", "spec", 1, -1, 1, 1, 0, 1);
h.SetBinContent(1, 1, 1);
generator->SetSpiecies(h, Hal::Const::PionPlusPID());
generator->SetFixMult(100);
source->AddEventGenerator(generator);
source->Register();
run->SetOutput("data.root");
run->SetSource(source);
run->Init();
run->Run();
}
Zaawansowany generator zderzeń
Parametry zderzeń
W fizyce ciężkich jonów istotnymi parametrami zderzeń są centralność, krotność, parametr zderzenia i kąt płaszczyzny reakcji. Na początku przyjmijmy standardową w tej fizyce konwencję, która mówi że jony poruszają się wzdłuż osi Z. Jak będzie wyglądało zderzenie w płaszczyźnie XY? Otóż mniej więcej tak:
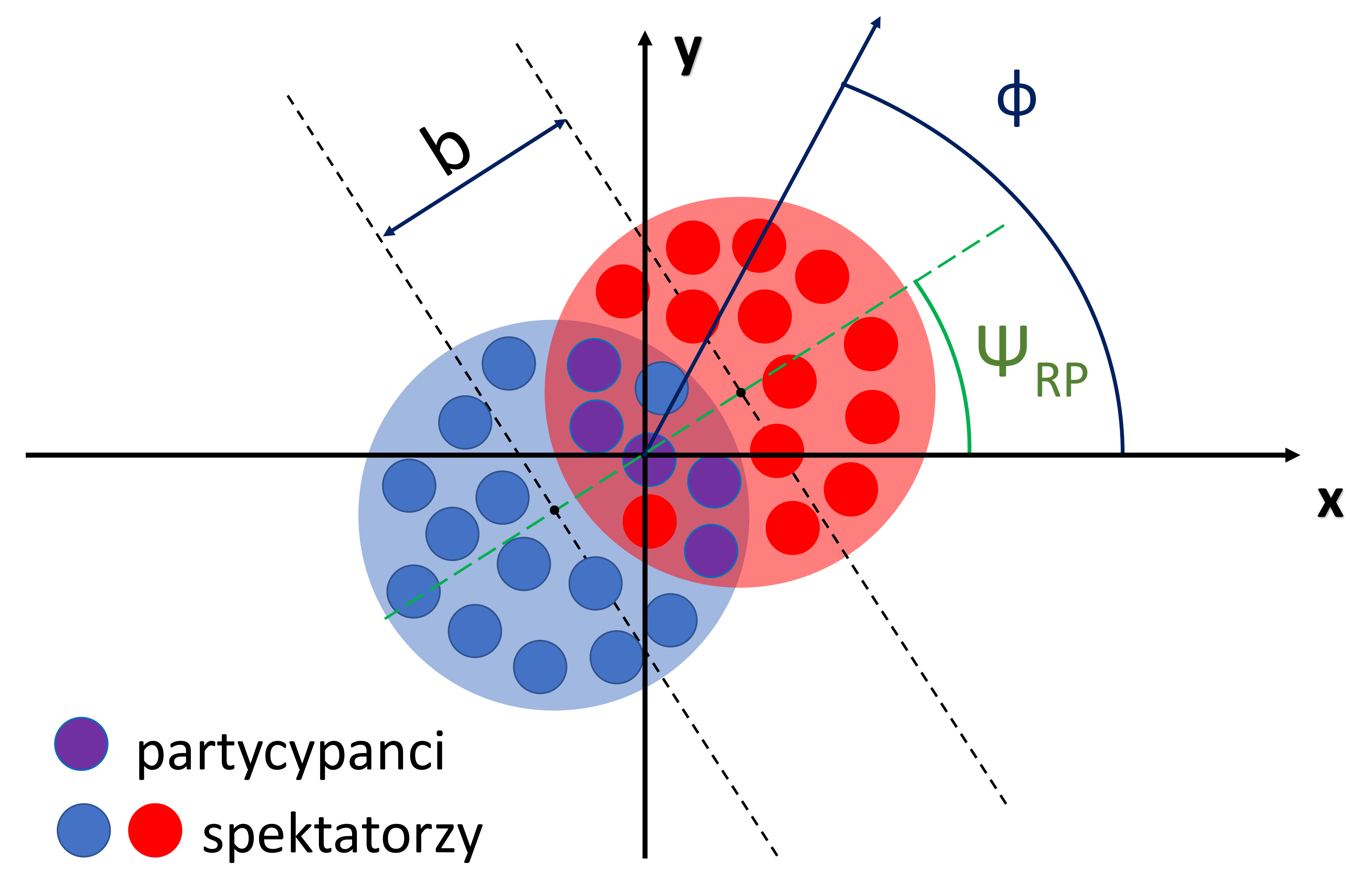
Widzimy tutaj dwa jony które się zderzają. Zauważyć można że w tym zderzeniu jony nie przekrywają się w 100%. Istnieje obszar przekrycia (fioletowy). W takim przypadku możemy wyróżnić:
dwa rodzaje nukleonów:partycypantów, którzy biorą udział w zderzeniu
spektatorów którzy choć wchodzą w skład zderzanych jonów, nie biorą udziału w zderzeniu
kąt płaszczyzny reakcji $\Psi_{RP}$, mówi on jaka jest orientacja zderzenia względem układu odniesienia detektora
parametr zderzenia b - mówi on jaka jest odległość między środkami zderzanych jonów w momencie kolizji
W eksperymencie nie kontrolujemy w zasadzie, żadnego z parametrów opisanych wyżej. Ważny natomiast jest ich pomiar gdyż właściwości zderzenia mocno zależą od tych parametrów. Przykładowo im mniejsze b tym większy obszar przekrycia - a więc więcej partycypantów i co za tym idzie więcej wyprodukowanych cząstek.
Wartość parametru zderzenia możemy oszacować przy pomocy krotności. Krotność to liczba wyprodukowanych w zderzeniu cząstek, ponieważ z reguły detektor nie mierzy wszystkich cząstek definiuje się czasem krotność jako liczbę zarejestrowanych cząstek albo np. liczbę zarejestrowanych cząstek w jakimś przedziale kinematycznym. Ogólną prawidłowością jest, że krotność rośnie gdy b maleje. Z krotnością łączy się też inny parametr - centralność. Centralność wyznacza się na podstawie krotności i opisuje ona ile % zderzeń ma większą krotność. Czyli jeśli nasze zderzenie ma maksymalną liczbę cząstek (krotność) to centralność wynosi 0%, jeśli połowa zderzeń ma większą krotność to centralność wynosi 50% itd. Zauważyć tu można, że najbardziej centralne zderzenia (b bliskie zeru) będą miały najmniejszą krotność.
Krotność, centralność parametr zderzenia
Można teraz się zastanowić jak będą się łączyć krotność, centralność i parametr zderzenia. Otóż jak pisałem będzie tak że np. mniejsza centralność to większa krotność ale ta zależność nie będzie liniowa. Na szczęście relatywnie prosto można sobie odtworzyć z grubsza tę zależność. Napiszemy tu własny model (jakby ktoś jednak chciał się pobawić z prawdziwym modelem to polecam model SMASH jest relatywnie prosty w instalacji i obsłudze).
No ale piszmy ten model. Model będzie uproszczony, będziemy tu zakładali że:
- w zasadzie nie interesują nas właściwości cząstek, toteż użyjemy modelu HalOTF::Generator z poprzedniego przypadku
- parametr zderzenia skaluje się liniowo tzn. $\rho(b)\approx ab$ gdzie $a$ jest jakąś stałą. Jest to dosyć dobre "geometryczne" przybliżenie które bazuje na założeniu, że mamy 2 zderzające się kółka. Zainteresowany może wyprowadzić tę zależność.
- nukleony w jądrze są rozłożone w sposób całkowicie chaotyczny
- liczba cząstek wyprodukowanych w kolizji jest taka sama jak liczba zderzeń partycypantów
- promień jądra atomowego to $R=r_0A^{1/3}$ gdzie $r_0=1.25\;fm$
- nukleony poruszają się po liniach prostych, ich kolizje nie zmieniają ich toru lotu
- kolizja między nukleonami zachodzi, gdy odległość między ich centrami wynosi mniej niż $r_0$
Poniżej kod generatora
struct particle {
double x;
double y;
};
class CustomGenerator : public HalOTF::EventGenerator {
Double_t fR = {0};
Double_t fA = 0;
std::vector nuc1;
std::vector nuc2;
Double_t GetB() {
Double_t rMax = 2.0 * fR;
double a = gRandom->Uniform();
double b = gRandom->Uniform();
while (b > a) {
a = gRandom->Uniform();
b = gRandom->Uniform();
}
return rMax * (1 - b);
}
void GenerateNucleus(Int_t flag, Double_t shift) {
double x, y, r;
for (int i = 0; i < fA; i++) {
r = 1E+9;
do {
x = gRandom->Uniform(-fR, fR);
y = gRandom->Uniform(-fR, fR);
double z = gRandom->Uniform(-fR, fR);
r = TMath::Sqrt(x * x + y * y + z * z);
} while (r > fR);
if (flag == 0) {
nuc1[i].x = x + shift;
nuc1[i].y = y;
} else {
nuc2[i].x = x + shift;
nuc2[i].y = y;
}
}
}
Int_t Collide() {
int nColl = 0;
for (auto& p1 : nuc1) {
for (auto& p2 : nuc2) {
double dx = p1.x - p2.x;
double dy = p1.y - p2.y;
double dist = TMath::Sqrt(dx * dx + dy * dy);
if (dist < 1.25) { nColl++; }
}
}
return nColl;
}
protected:
virtual void GenerateEvent() {
Double_t b = GetB();
GenerateNucleus(0, b * 0.5);
GenerateNucleus(1, -b * 0.5);
fFixedMultiplicity = Collide();
HalOTF::EventGenerator::GenerateEvent();
fMcEvent->SetB(b);
}
public:
CustomGenerator() {};
void SetA(Int_t a) {
fR = 1.25 * TMath::Power(a, 1. / 3.);
fA = a;
nuc1.resize(a);
nuc2.resize(a);
}
virtual ~CustomGenerator() {};
};
Funkcja GetB zwraca nam parametr zderzenia. Jest to klasyczny algorytm MC - losujemy parę zmiennych a i b, tak długo jak $a<\rho(b)$. W funkcji Generate Nucleus generujemy położenia protonów i neutronów w danym jądrze, pozycję przesuwamy o wartość shift (jest to połowa parametru zderzenia).Tu dla uproszczenia zakładam, że kąt płaszczyzny reakcji wynosi zawsze 0. Generacja bazuje na podobnej metodzie MC - generujemy 3 współrzędne losowe tak długo aż nasze koordynaty nie znajdą się we wnętrzu kuli reprezentującej jon. Funkcja collide oblicza ilość kolizji.
W funkcji GenerateEvent wyznaczamy parametr zderzenia B, generujemy położenia nukleonów, a następnie symulujemy kolizję. Mając liczbę zderzeń partycypantów nadpisujemy zmienną fFixedMultiplicity wymuszając generację odpowiedniej ilości zderzeń. Ustawiamy też parametr zderzenia B w opisie zderznia MC. Na koniec zostaje nam metoda SetA gdzie ustawiamy liczbę nukleonów w zderzanych jądrach atomowych, oraz wyliczamy promień jądra.
Aby wygenerować sobie dane wystarczy użyć makra:
void glauber_gen() {
auto run = new Hal::AnalysisManager();
auto source = new HalOTF::Source(10000);
auto generator = new CustomGenerator;
TH2D h("spec", "spec", 1, -1, 1, 1, 0, 1);
h.SetBinContent(1, 1, 1);
generator->SetSpiecies(h, Hal::Const::PionPlusPID());
generator->SetFixMult(100);
generator->SetA(197);
source->AddEventGenerator(generator);
source->Register();//w ten sposób zapisujemy dane do pliku wyjściowego
run->SetOutput("/opt/temp/glauber.root");
run->SetSource(source);
run->Init();
run->Run();
}
W części następnej zobaczymy co otrzymamy w wyniku analizy takich zderzeń.